Google Data

Arno Eigenwillig, Software Engineer on Google Maps Directions

What is the best way to get from A to B by public transit? Google Maps is answering such queries for over 20,000 cities and towns in over 70 countries around the world, including large metro areas like New York, São Paulo or Moscow, and some complete countries, such as Japan or Great Britain.
Since its beginnings in 2005 with the single city of Portland, Oregon, the number of cities and countries served by Google’s public transit directions has been growing rapidly. With more and larger regions, the amount of data we need to search in order to provide optimal directions has grown as well. In 2010, the search speed of transit directions made a leap ahead of that growth and became fast enough to update the result while you drag the endpoints. The technique behind that speed-up is the Transfer Patterns algorithm [1], which was created at Google’s engineering office in Zurich, Switzerland, by visiting researcher Hannah Bast and a number of Google engineers.

I am happy to report that this research collaboration has continued and expanded with the Google Focused Research Award on Next-Generation Route Planning. Over the past three years, this grant has supported Hannah Bast’s research group at the University of Freiburg, as well as the research groups of Peter Sanders and Dorothea Wagner at the Karlsruhe Institute of Technology (KIT).

From the project’s numerous outcomes, I’d like to highlight two recent ones that re-examine the Transfer Patterns approach and massively improve it for continent-sized networks: Scalable Transfer Patterns [2] and Frequency-Based Search for Public Transit [3] by Hannah Bast, Sabine Storandt and Matthias Hertel. This blogpost presents the results from these publications.

The notion of a transfer pattern is easy to understand. Suppose you are at a transit stop downtown, call it A, and want to go to some stop B as quickly as possible. Suppose further you brought a printed schedule book but no smartphone. (This sounded plausible only a few years ago!) As a local, you might know that there are only two reasonable options:

1. Take a tram from A to C, then transfer at C to a bus to B.
2. Take the direct bus from A to B, which only runs infrequently.

We say the first option has transfer pattern A-C-B, and the second option has transfer pattern A-B. Notice that no in-between stops are mentioned. This is very compact information, much less than the actual schedules, but it makes looking up the schedules significantly faster: Knowing that all optimal trips follow one of these patterns, you only need to look at those lines in the schedule book that provide direct connections from A to C, C to B and A to B. All other lines can safely be ignored: you know you will not miss a better option.

While the basic idea of transfer patterns is indeed that simple, it takes more to make it work in practice. The transfer patterns of all optimal trips have to be computed ahead of time and stored, so that they are available to answer queries. Conceptually, we need transfer patterns for every pair of stops, because any pair could come up in a query. It is perfectly reasonable to compute them for all pairs within one city, or even one metro area that is densely criss-crossed by a transit network comprising, say, a thousand stops, yielding a million of pairs to consider.

As the scale of the problem increases from one metro area to an entire country or continent, this “all pairs” approach rapidly becomes expensive: ten thousand stops (10x more than above) already yield a hundred million pairs (100x more than above), and so on. Also, the individual transfer patterns become quite repetitive: For example, from any stop in Paris, France to any stop in Cologne, Germany, all optimal connections end up using the same few long-distance train lines in the middle, only the local connections to the railway stations depend on the specific pair of stops considered.

However, designated long-distance connections are not the only way to travel between different local networks – they also overlap and connect to each other. For mid-range trips, there is no universally correct rule when to choose a long-distance train or intercity bus, short of actually comparing options with local or regional transit, too.

The Scalable Transfer Patterns algorithm [2] does just that, but in a smart way. For starters, it uses what is known as graph clustering to cut the network into pieces, called clusters, that have a lot of connections inside but relatively few to the outside. As an example, the figure below (kindly provided by the authors) shows a partitioning of Germany into clusters. The stops highlighted in red are border stops: They connect directly to stops outside the cluster. Notice how they are a small fraction of the total network.

The public transit network of Germany (dots and lines), split into clusters (shown in various colors). Of all 251,763 stops, only 10,886 (4.32%) are boundary stops, highlighted as red boxes. Click here to view the full resolution image.[source: S. Storandt, 2016]

Based on the clustering, the transfer patterns of all optimal connections are computed in two steps.

In step 1, transfer patterns are computed for optimal connections inside each cluster. They are stored for query processing later on, but they also accelerate the search through a cluster in the following step: between the stops on its border, we only need to consider the connections captured in the transfer patterns.

The next figure sketches how the transit network in the cluster around Berlin gets reduced to much fewer connections between border stations. (The central station stands out as a hub, as expected. It is a border station itself, because it has direct connections out of the cluster.)

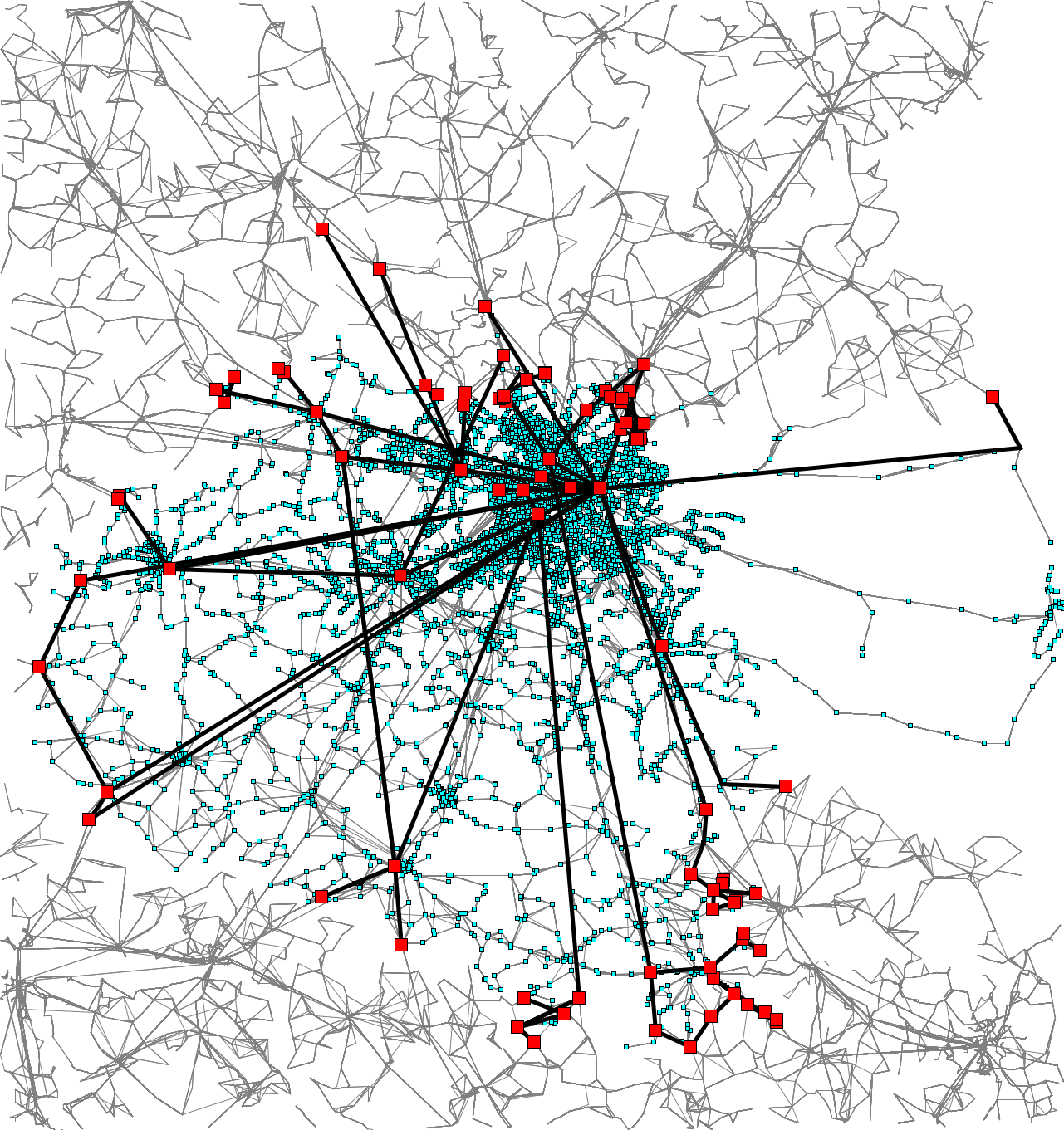The cluster of public transit connections around Berlin (shown as dots and lines in light blue), its border stops (highlighted as red boxes), and the transfer patterns of optimal connections between border stops (thick black lines; only the most important 111 of 592 are shown to keep the image legible). This cuts out 96.15% of the network (especially a lot of the high-frequency inner city trips, which makes the time savings even bigger). Click here to view the full resolution image. [source: S. Storandt, 2016]

In step 2, transfer patterns can be computed for the entire network, that is, between any pair of clusters. This is done with the following twists:

• It suffices to consider trips from and to boundary stops of any cluster; the local transfer patterns from step 1 will supply the missing pieces later on.
• The per-cluster transfer patterns from step 1 greatly accelerate the search across other clusters.
• The search stops exploring any possible connection between two boundary stops as soon as it gets worse than a connection that sticks to long-distance transit between clusters (which may not always be optimal, but is always quick to compute).

The results of steps 1 and 2 are stored and used to answer queries. For any given query from some A to some B, one can now easily stitch together a network of transfer patterns that covers all optimal connections from A to B. Looking up the direct connections on that small network (like in the introductory example) and finding the best one for the queried time is very fast, even if A and B are far away.

The total storage space needed for this is much smaller than the space that would be needed for all pairs of stops, all the more the larger the network gets. Extrapolating from their experiments, the researchers estimate [2] that Scalable Transfer Patterns for the whole world could be stored in 30 GB, cutting their estimate for the basic Transfer Patterns by a thousand(!). This is considerably more powerful than the “hub station” idea from the original Transfer Patterns paper [1].

The time needed to compute Scalable Transfer Patterns is also estimated to shrink by three orders of magnitude: At a high level, the earlier phases of the algorithm accelerate the later ones, as described above. At a low level, a second optimization technique kicks in: exploiting the repetitiveness of schedules in time. Recall that finding transfer patterns is all about finding the optimal connections between pairs of stops at any possible departure time.

Frequency-based schedules (e.g., one bus every 10 minutes) cause a lot of similarity during the day, although it often doesn’t match up between lines (e.g., said bus runs every 10 minutes before 6pm and every 20 minutes after, and we seek connections to a train that runs every 12 minutes before 8pm and every 30 minutes after). Moreover, this similarity also exists from one day to the next, and we need to consider all permissible departure dates.

The Frequency-Based Search for Public Transit [3] is carefully designed to find and take advantage of repetitive schedules while representing all one-off cases exactly. Comparing to the set-up from the original Transfer Patterns paper [1], the authors estimate a whopping 60x acceleration of finding transfer patterns from this part alone.

I am excited to see that the scalability questions originally left open by [1] have been answered so convincingly as part of this Focused Research Award. Please see the list of publications on the project’s website for more outcomes of this award. Besides more on transfer patterns, they contain a wealth of other results about routing on road networks, transit networks, and with combinations of travel modes.

References:

[1] Fast Routing in Very Large Public Transportation Networks Using Transfer Patterns
by H. Bast, E. Carlsson, A. Eigenwillig, R. Geisberger, C. Harrelson, V. Raychev and F. Viger
(ESA 2010). [doi]

[2] Scalable Transfer Patterns
by H. Bast, M. Hertel and S. Storandt (ALENEX 2016). [doi]

[3] Frequency-based Search for Public Transit
by H. Bast and S. Storandt (SIGSPATIAL 2014). [doi]